盛最多水的容器（蓄水池问题）

1721 字

本期题解：LeetCode 11 - Container With Most Water（Medium）

给定 $n$ 个非负整数 $a_1, a_2, \dots, a_n$ ，每个数代表坐标中的一个点 $(i, a_i)$ 。在坐标内画 $n$ 条竖直线，竖直线 $i$ 的两个端点分别为 $(i, a_i)$ 和 $(i, 0)$ 。找出其中的两条线，使得它们与 $x$ 轴共同构成的容器可以容纳最多的水。

说明： 你不能倾斜容器，且 $n$ 的值至少为 2。

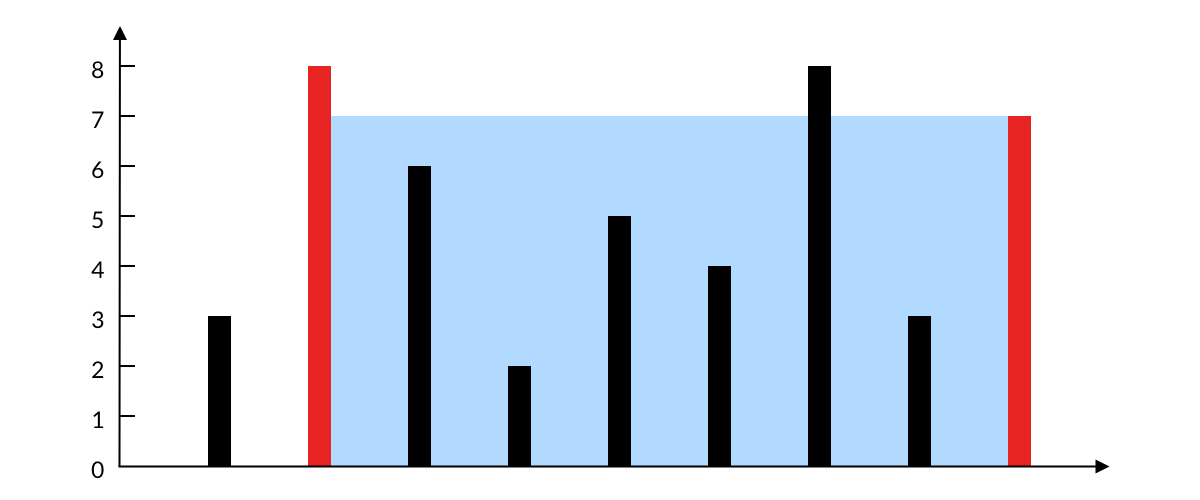
图中垂直线代表输入数组 [3,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

这道题在 LeetCode 中排序很靠前，相信你们都见过这道题目。题意理解起来很简单，但要做出来并不容易，尤其是得到 $O(n)$ 时间复杂度的解法。即使看了答案知道了 $O(n)$ 解法怎么做，也不一定能证明它的正确性。

很多人没有发现，这道题其实和 167 题 Two Sum II 极其相似。两道题从描述上看起来没有什么联系，但是解法和正确性证明几乎一样。在上一篇 LeetCode 例题精讲第四讲中，我使用的例题正是 Two Sum II 问题，而这道盛水容器问题正是放在了相关题目中。

本期的题解和 Two Sum II 的题解紧密相关。如果你忘记了 Two Sum II 问题是什么，或者忘记了它的解法，强烈建议你先阅读上篇文章中的讲解：

LeetCode 例题精讲 | 04 用双指针解 Two Sum：缩减搜索空间

解法

从复杂度倒推解法

本题的暴力解法很容易得到，只需要穷举所有柱子的两两组合，对每个组合都计算一次容纳水的面积即可。暴力法的时间复杂度是 $O(n^2)$ 。

很显然，这个暴力法不会是最终的正确答案。那么我们必须做到比 $O(n^2)$ 的时间复杂度更小，基本上只可能是 $O(n \log n)$ 或 $O(n)$ 的复杂度。

如果是 $O(n \log n)$ 的话，肯定是使用分治法。但是分治法需要把问题规模切分，而大量的柱子两两组合落在切分后的左右两侧，不好处理。所以分治法不好做。

如果是 $O(n)$ 的话，我们首先会想到动态规划解法。但是动态规划的子问题之间似乎没什么关系。容纳水的面积只和左右的两个柱子的高度有关，和其他柱子没什么关系。既然找不到子问题之间的关系，我们也就不好使用动态规划方法。

看起来似乎走投无路了？没关系，我们还有一招双指针方法，这个方法在上篇文章中刚刚讲过。

双指针解法

和 Two Sum II 类似，这道题的搜索空间大小是 $O(n^2)$ 数量级。暴力法一次考察搜索空间中的一个情况，时间复杂度自然也是 $O(n^2)$ 。而我们希望用一种方法，一次排除多个情况，从而减少时间复杂度。

在一开始，我们考虑相距最远的两个柱子所能容纳水的面积。水的宽度是两根柱子之间的距离 $d = 8$ ；水的高度取决于两根柱子之间较短的那个，即左边柱子的高度 $h = 3$ 。水的面积就是 $3 \times 8 = 24$ 。

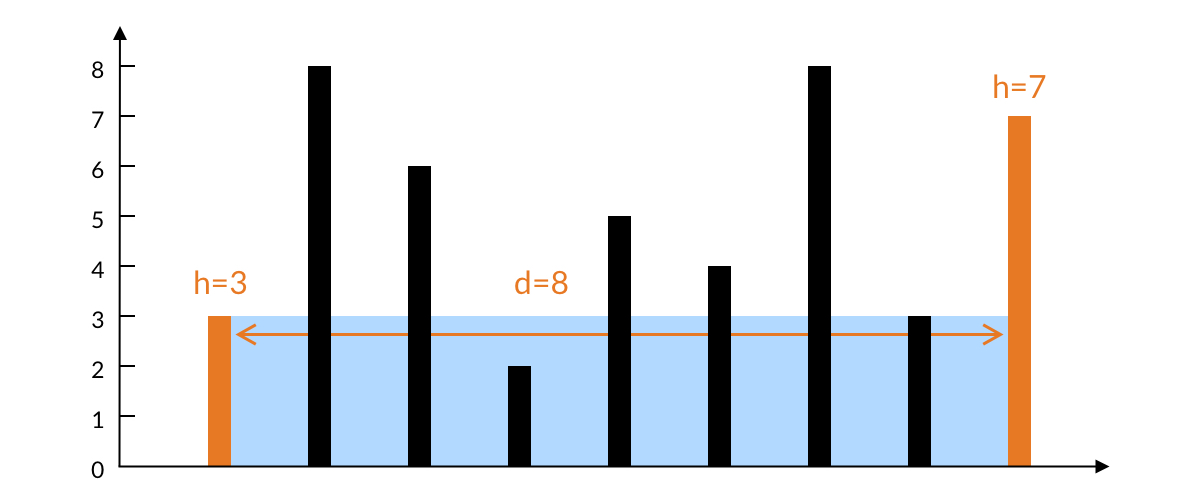
相距最远的两个柱子容纳水的面积

如果选择固定一根柱子，另外一根变化，水的面积会有什么变化吗？稍加思考可得：

当前柱子是最两侧的柱子，水的宽度 $d$ 为最大，其他的组合，水的宽度都比这个小。
左边柱子较短，决定了水的高度为 3。如果移动左边的柱子，新的水面高度不确定，一定不会超过右边的柱子高度 7。
如果移动右边的柱子，新的水面高度一定不会超过左边的柱子高度 3，也就是不会超过现在的水面高度。

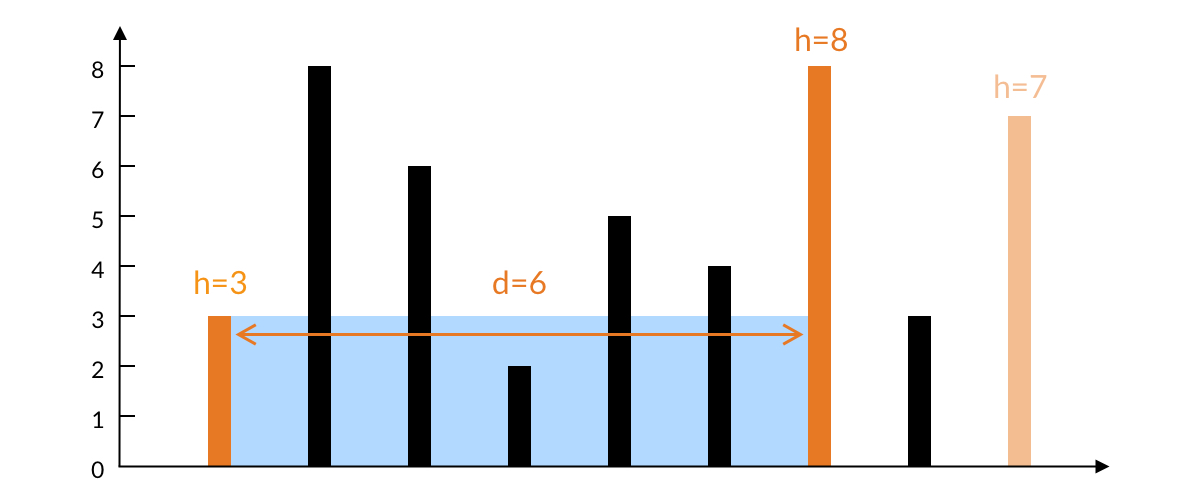
移动右边柱子时水的面积变化

由此可见，如果固定左边的柱子，移动右边的柱子，那么水的高度一定不会增加，且宽度一定减少，所以水的面积一定减少。这个时候，左边的柱子和任意一个其他柱子的组合，其实都可以排除了。也就是我们可以排除掉左边的柱子了。

排除左边这个柱子的操作，对应于双指针解法的代码，就是指针向右移动一位。对应于搜索空间，就是削减了一行的搜索空间，如下图所示。

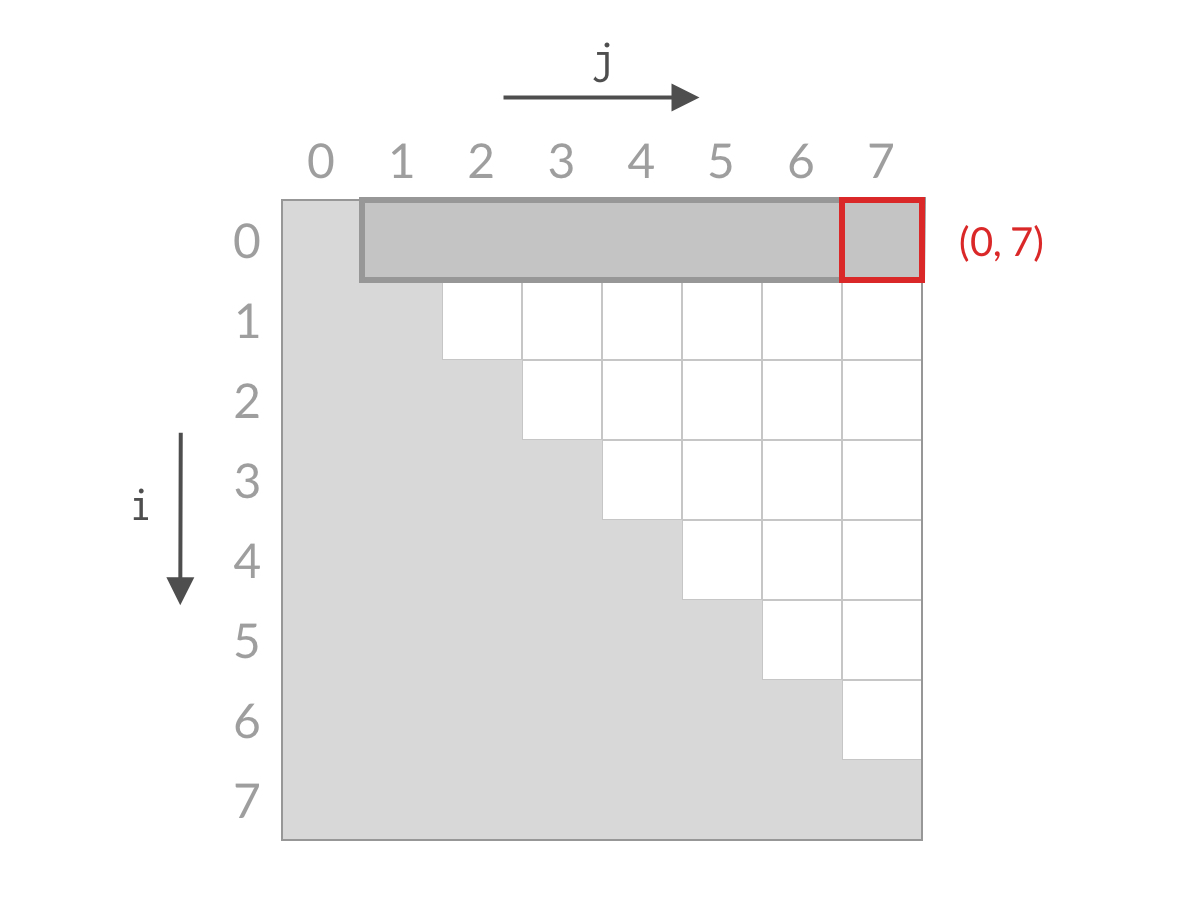
削减一行的搜索空间

可以看到，这个搜索空间的削减方式和 Two Sum II 问题中的形状如出一辙（其实就是我把上一篇文章里的图直接搬过来了），如果你理解了 Two Sum II 问题，那一定能秒懂这道题。

同样的道理，假设两根柱子是右边的较短，我们就可以排除掉右边的柱子，削减一列的搜索空间，如下图所示。

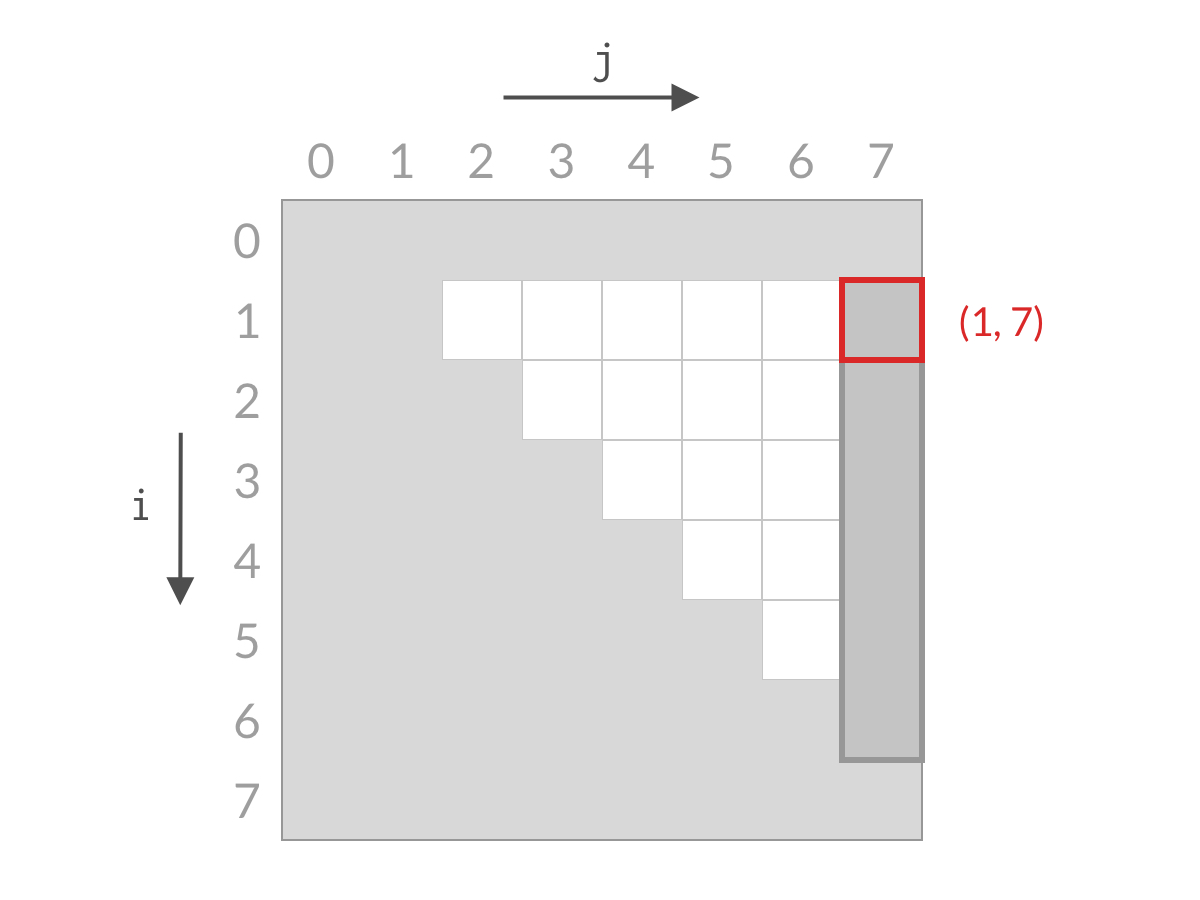
削减一列的搜索空间

这样，经过 $n$ 步以后，我们就能排除所有的搜索空间，检查完所有的可能性。

那么，我们最终就写出了这样的双指针代码：

public int maxArea(int[] height) {
    int res = 0;
    int i = 0;
    int j = height.length - 1;
    while (i < j) {
        int area = (j - i) * Math.min(height[i], height[j]);
        res = Math.max(res, area);
        if (height[i] < height[j]) {
            i++;
        } else {
            j--;
        }
    }
    return res;
}

总结

实话说，很少有人能在第一次接触到这一题的时候就立即想出这样巧妙的双指针解法，所以刷题提升的过程一定是伴随着“记答案”的。但是我们同时还要善于归纳和总结，因为死记硬背是个苦工夫，只有理解了思想，才能记得快、记得牢。

就比如 167 题的 Two Sum II 和这道题。两者都是用这样的双指针解法，从代码上看非常相似，但它们究竟为何相似呢？实际上，两道题就是因为削减搜索空间的原理相通，解题思路实际上是一模一样的。如果你能洞察这一点，那么距离举一反三也就不远了。

解法
- 从复杂度倒推解法
- 双指针解法
总结