最大子数组和：子数组类问题的动态规划技巧

2848 字

本期例题：

LeetCode 53. Maximum Subarray Sum 最大子数组和（Easy）
LeetCode 718. Maximum Length of Repeated Subarray 最长公共子数组（Medium）

在前面的文章中，我们分别讲解了一维和二维动态规划问题的解题步骤与基本思路。不过，仅仅掌握基本步骤是不够的。要想熟练做出动态规划题目，还要掌握足够的解题技巧。

接下来的文章中，我会讲解动态规划问题中针对不同类型问题的小技巧。今天要讲的是关于「子数组」类题目的常见技巧。

在讲具体问题之前，我们要明确一下「子数组」和「子序列」的概念。

子序列 (subsequence) 可以是不连续的。例如 "ACD" 是 "ABCDE" 的子序列；
子数组 (subarray)、子串 (substring) 必须是连续的。例如 "BCD" 是 "ABCDE" 的子数组/子串。

我们前面的例题中讲过的最长公共子序列问题，关注的是「子序列」，而今天的文章我们要关注的都是「子数组」，请牢记这一点。

这篇文章的内容包括：

子数组类问题的动态规划技巧
「最大子数组和」问题的解法
「最长公共子数组」问题的解法

最大子数组和

LeetCode 53. Maximum Subarray Sum 最大子数组和（Easy）

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例:
输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

子问题定义的错误尝试

拿到这道「最大子数组和」问题，如果直接把动态规划的解题四步骤往上套，那么你可能首先会想到这么定义子问题：

子问题 $f(k)$ 表示「nums[0..k) 中的最大子数组和」。

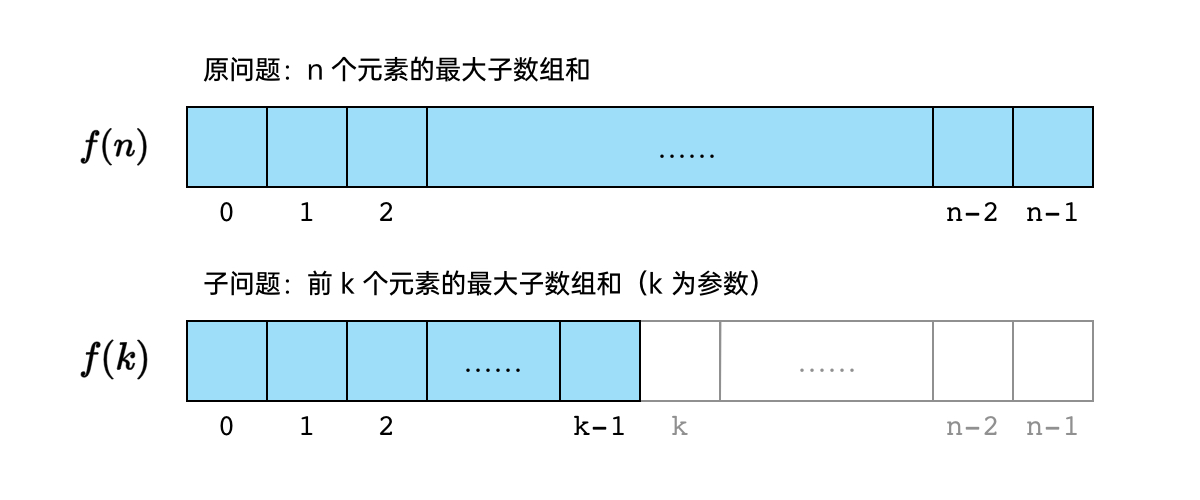
子问题定义的尝试

很不幸，这么定义子问题是行不通的。因为这么定义的话，我们无法写出子问题的递推关系！

我们用一个实际的例子 [-1, 2, 3, -2, 4, 1] ，看看每个子问题计算的结果：

$f(1)$ 即 [-1] 的最大和子数组为 [-1]，和为 -1；
$f(2)$ 即 [-1, 2] 的最大和子数组为 [2]，和为 2；
$f(3)$ 即 [-1, 2, 3] 的最大和子数组为 [2, 3]，和为 5；
$f(4)$ 即 [-1, 2, 3, -2] 的最大和子数组为 [2, 3]，和为 5；
$f(5)$ 即 [-1, 2, 3, -2, 4] 的最大和子数组为 [2, 3, -2, 4]，和为 7；
$f(6)$ 即 [-1, 2, 3, -2, 4, 1] 的最大和子数组为 [2, 3, -2, 4, 1]，和为 8。

在依次计算子问题的过程中， $f(4)$ 到 $f(5)$ 的递推关系出现了一个断裂：

$f(4)$ 求出 [-1, 2, 3, -2] 的最大和子数组和为 [2, 3]，位于数组的中部。

求 $f(5)$ 的时候，我们加入了一个新元素 4。自然地，我们想知道这个新元素能不能与 $f(4)$ 求出的最优解相结合，得到 $f(5)$ 的最优解。然而，它们结合不起来！

$f(4)$ 的最优解 [2, 3]，和新元素 4 并不相邻。它们不能拼成一个连续的子数组！

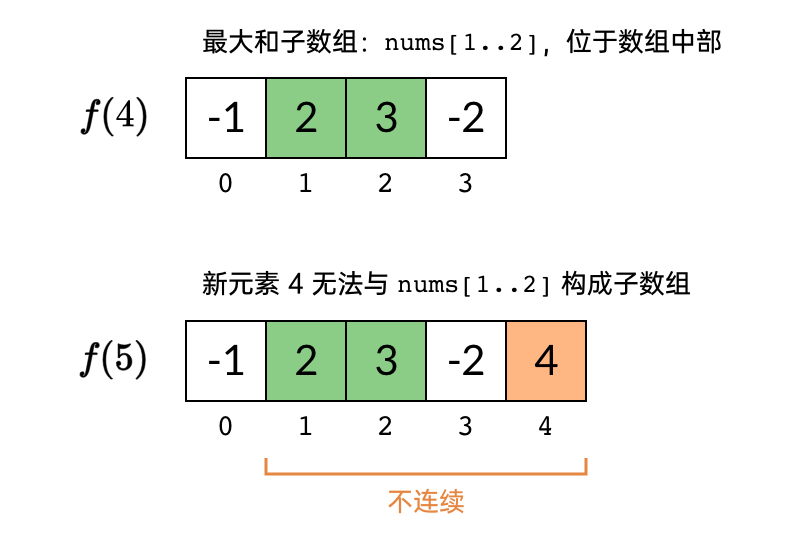
尝试构造子问题的递推关系

可见，问题出在「子数组」的限制上。子数组要求元素是连续的，那么，前一个子问题的最优解，可能在后一个子问题中用不上。子问题的递推链条就断开了。

正确的子问题定义

那么，怎么解决这个子问题「续不上」的问题呢？答案是修改子问题的定义，加一个限制条件：

子问题 $f(k)$ 表示「nums[0..k) 中，以最后一个元素结尾的最大子数组和」。

既然子数组拼接不起来，那么我们就限制子问题计算的子数组只能位于数组尾部。这样得到的最大和子数组，就一定可以跟下一个元素拼接起来了。

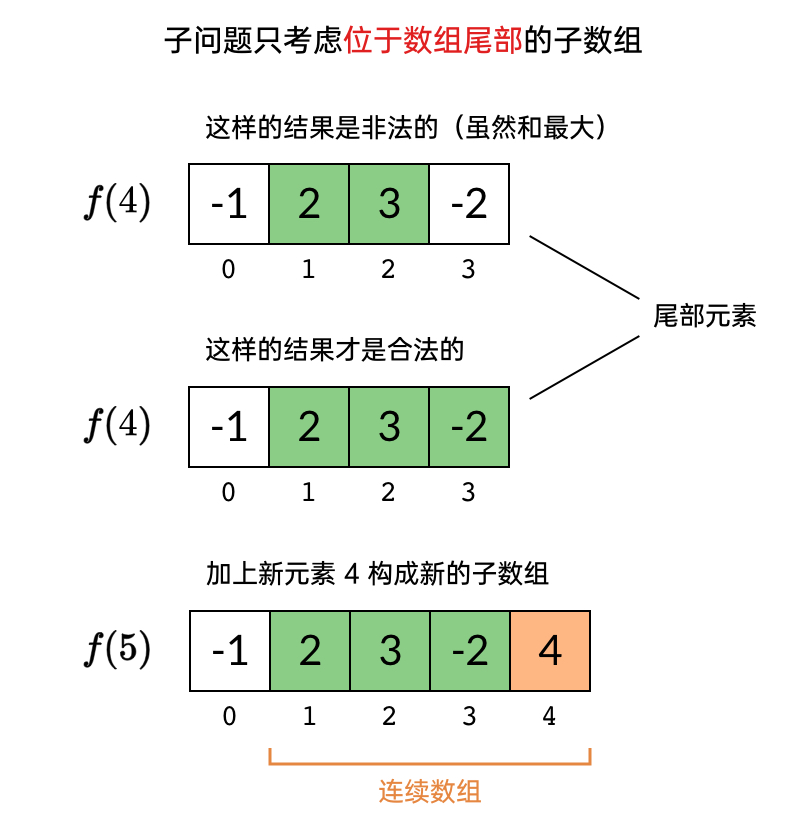
子问题的新版定义

我们来看看这时候的子问题是怎么计算的：

$f(4)$ 这时候求的是 [-1, 2, 3, - 2] 中位于数组尾部的最大子数组和，结果是 [2, 3, -2]，和为 3。
计算 $f(5)$ 的时候，直接把新元素 4 跟前面的最优解 [2, 3, -2] 拼接起来，得到最大和子数组是 [2, 3, -2, 4]，和为 7。

子问题的递推关系

正确定义了子问题，就可以写出子问题的递推关系了。我们用 $n_i$ 表示元素 nums[i]，写出的子问题递推公式为：

f(k) = \max \begin{cases} f(k-1) + n_{k-1} \\ n_{k-1} \end{cases}

这个递推公式的含义是，计算 nums[0..k) 的最大子数组和时，要么是把新元素 nums[k-1] 加入前一个子问题的结果（即 $f(k-1) + n_{k-1}$ 的含义），要么是只使用元素 nums[k-1]，选择其中结果较大的一个方案。

这个递推公式可以继续化简为：

f(k) = \max \{ f(k-1), 0 \} + n_{k-1}

这样，我们就可以写出题解代码了：

public int maxSubArray(int[] nums) {
    // 子问题：
    // f(k) = nums[0..k) 中以 nums[k-1] 结尾的最大子数组和
	// 原问题 = max{ f(k) }, 0 <= k <= N

    // f(0) = 0
    // f(k) = max{ f(k-1), 0 } + nums[k-1]

    int N = nums.length;
    int[] dp = new int[N+1];
    dp[0] = 0;

    int res = Integer.MIN_VALUE;
    for (int k = 1; k <= N; k++) {
        dp[k] = Math.max(dp[k-1], 0) + nums[k-1];
        res = Math.max(res, dp[k]);
    }
    return res;
}

需要注意的是，我们最后不能直接返回最后一个子问题 $f(n)$ 的结果。因为我们子问题的定义变了， $f(n)$ 只计算了以最后一个元素结尾的最大子数组和。我们需要取所有子问题结果的最大值，也就是

最终结果 = \max_{0 \le k \le n} f(k)

限于文章篇幅，我们这里就不讨论这道题的空间优化方法以及其他解法了。以后会专门写一篇文章介绍这道题的不同解法。

最长公共子数组

理解了「最大子数组和」问题的解法，我们再来看一道类似思路的二维动态规划问题：最长公共子数组。

LeetCode 718. Maximum Length of Repeated Subarray 最长公共子数组（Medium）

给两个整数数组 s 和 t ，返回两个数组中公共的、长度最长的子数组的长度。例如：
输入:
s: [1, 2, 3, 2, 1, 5]
t: [6，3, 2, 1, 4, 7]
输出: 3
解释: 
长度最长的公共子数组是 [3, 2, 1]。

「最长公共子数组」问题其实和「最长公共子序列」问题相似，只是把题目中的「子序列」换成了「子数组」。如果你对「最长公共子序列」问题不是很熟悉，可以回顾之前的文章：

LeetCode 例题精讲 | 15 最长公共子序列：二维动态规划的解法

在「最长公共子序列」问题中，我们是这样定义子问题的：

子问题 $f(i, j)$ 表示「s[0..i) 和 t[0..j) 的最长公共子序列」。

然而，当问题变成「子数组」以后，子数组的性质导致了原先的子问题递推关系不成立了，我们需要重新定义子问题。我们参考上一道例题的方法，给子数组加上一个位于数组尾部的限制，将子问题定义成这样：

子问题 $f(i, j)$ 表示「s[0..i) 和 t[0..j) 中，以最后一个元素结尾的最长公共子数组」。

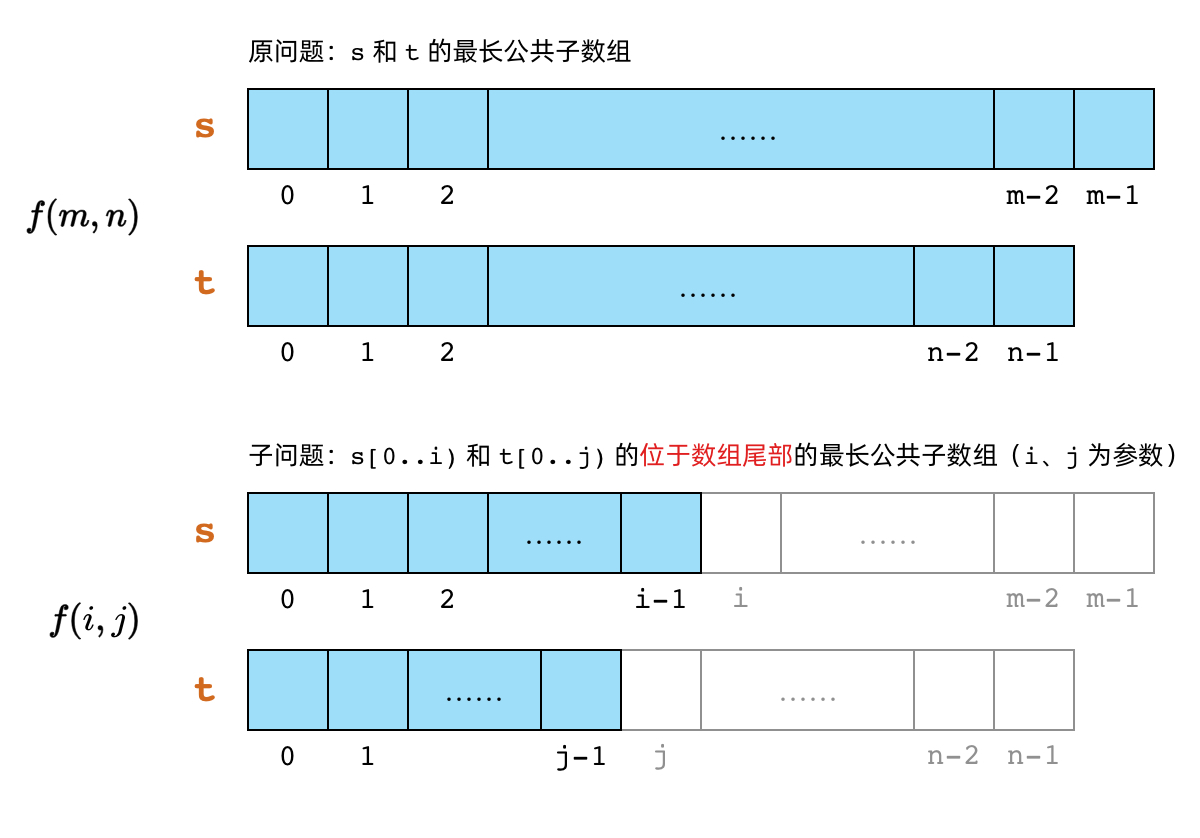
最长公共子数组问题的子问题定义

注意，这里的以最后一个元素结尾指的是公共子数组既要包含 s[0..i) 的最后一个元素，也要包含 t[0..j) 的最后一个元素。

换句话说，就是从后往前看 s[0..i) 和 t[0..j) 的最后有几个元素是相同的。

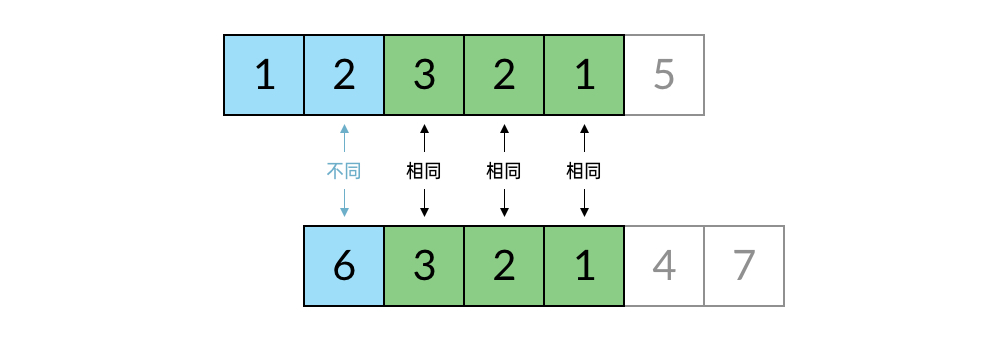
从后往前比较相同元素

那么子问题的递推关系如何定义呢？很简单，我们还是只需要看 s[0..i) 和 t[0..j) 的最后一个元素：s[i-1] 和 t[j-1]。

如果 s[i-1] == t[j-1]，那么已经有一个元素是相同的，接下来是要继续往前看 s[0..i-1) 和 t[0..j-1) 的最后有几个元素是相同的。也就是 $f(i, j) = f(i-1, j-1) + 1$ 。
如果 s[i-1] != t[j-1]，那么最后一个元素就不相同，前面就更不用看了。也就是 $f(i, j) = 0$ 。

这样我们就得到了子问题的递推公式：

f(i, j) = \begin{cases} f(i-1, j-1) + 1, & \text{if } s_{i-1} = t_{j-1} \\ 0, & \text{if } s_{i-1} \ne t_{j-1} \\ \end{cases}

那么原问题如何由子问题表示呢？是这样的：

最终结果 = \max_{0 \le i \le m, 0 \le j \le n} f(i, j)

这样，我们就可以写出题解代码了：

public int findLength(int[] s, int[] t) {
    // 子问题：
    // f(i, j) = s[0..i) 和 t[0..j) 中以 s[i-1] 和 t[j-1] 结尾的最长公共子数组
    // 原问题 = max{ f(i, j) }, 0 <= i <= m, 0 <= j <= n

    // f(0, *) = 0
    // f(*, 0) = 0
    // f(i, j) = max:
    //           f(i-1, j-1) + 1, if s[i-1] == t[j-1]
    //           0              , if s[i-1] != t[j-1]

    int m = s.length;
    int n = t.length;
    int[][] dp = new int[m+1][n+1];

    int res = 0;
    for (int i = 0; i <= m; i++) {
        for (int j = 0; j <= n; j++) {
            if (i == 0 || j == 0) {
                dp[i][j] = 0;
            } else {
                if (s[i-1] == t[j-1]) {
                    dp[i][j] = dp[i-1][j-1] + 1;
                } else {
                    dp[i][j] = 0;
                }
            }
            res = Math.max(res, dp[i][j]);
        }
    }
    return res;
}

总结

从以上两个例题中，我们可以看出「子数组」类问题的解题套路。我们可以在定义子问题的时候加上位于数组尾部的限制条件。这样才可以正常地推导出子问题的递推关系。

本文讲解的第二个例题「最长公共子数组」和「最长公共子序列」仅仅一个概念上的差距，子问题的定义和递推关系就有很多不同。建议大家把这两道题对照着来做，可以很容易地体会到「子数组」和「子序列」问题的不同之处。这里放上两道题的题号：

LeetCode 1143. Longest Common Subsequence 最长公共子序列（Medium）
LeetCode 718. Maximum Length of Repeated Subarray 最长公共子数组（Medium）

除了例题之外，LeetCode 上还有一些「子数组」类的题目：

LeetCode 152. Maximum Subarray Product 最大乘积子数组（Medium）
LeetCode 978. Longest Turbulent Subarray 最长波形子数组（Medium）

都是很典型的子数组类题目，可以试着练习一下。

我是 nettee，致力于分享面试算法的解题套路，让你真正掌握解题技巧，做到举一反三。我的《LeetCode 例题精讲》系列文章正在写作中，关注我的公众号，获取最新文章。

最大子数组和
最长公共子数组
总结