链表综合题：链表排序

2147 字

用 $O(n \log n)$ 级别的时间复杂度、常数级空间复杂度，对链表进行排序。

这个系列到目前为止已经讲了两期链表类问题了，分别是第一期的链表遍历框架、第五期的链表快慢指针。链表类问题并不复杂，这两大方法已经可以基本涵盖大部分的链表题目了。

本期所讲的链表排序问题是一道经典的链表综合题。在面试中，这道题非常常见，甚至是微软某面试官常用的”三板斧“之一，足以看出它的普适性。这道题需要用到链表问题各种常见的方法和操作。同时，它又涉及到将传统的数组排序方法迁移到链表，可以考察面试者对排序算法的理解。

具体来说，链表排序这道题可以考察：

对链表性质的掌握
对分治法的掌握
对链表操作的掌握

下面我们逐一讨论其中的要点。

排序思路

选择排序方法

首先，我们要理解链表问题的基本原则，不使用额外的空间。有的同学看到题目觉得难，就直接把链表转化成数组，然后对数组排序。这种做法显然是不合格的。链表问题中的不使用额外空间，在于不创建额外数组、不创建新的链表结点，也就是说，不使用 new 关键字。

明确了这个原则之后，我们再来看这道题目。题目要求使用 $O(n \log n)$ 级别的排序算法。回顾我们学过的排序算法，很显然，我们需要在快速排序、归并排序、堆排序中进行选择。

链表相对于数组最大的不同，在于链表只能进行顺序访问，甚至只能进行正向顺序访问，不能进行随机访问（按下标访问）。而考虑到快速排序、堆排序都涉及到大量的随机访问，必然排除。剩下的归并排序，仔细思考之后，确实可以只用顺序访问。那么，我们可以将归并排序方法应用到链表排序上。

将归并排序迁移到链表

如何将归并排序迁移到链表呢？我们需要回顾归并排序整个的过程。归并排序是一个典型的分治算法，和一般的分治法一样，有分、治、合三个步骤。

划分：将数组平分为左右两半， $O(1)$ 的时间；
递归：对左右两半的数组分别递归排序，每一半是 $n/2$ 的问题规模；
合并：将左右已排序的数组合并为一个， $O(n)$ 的时间。

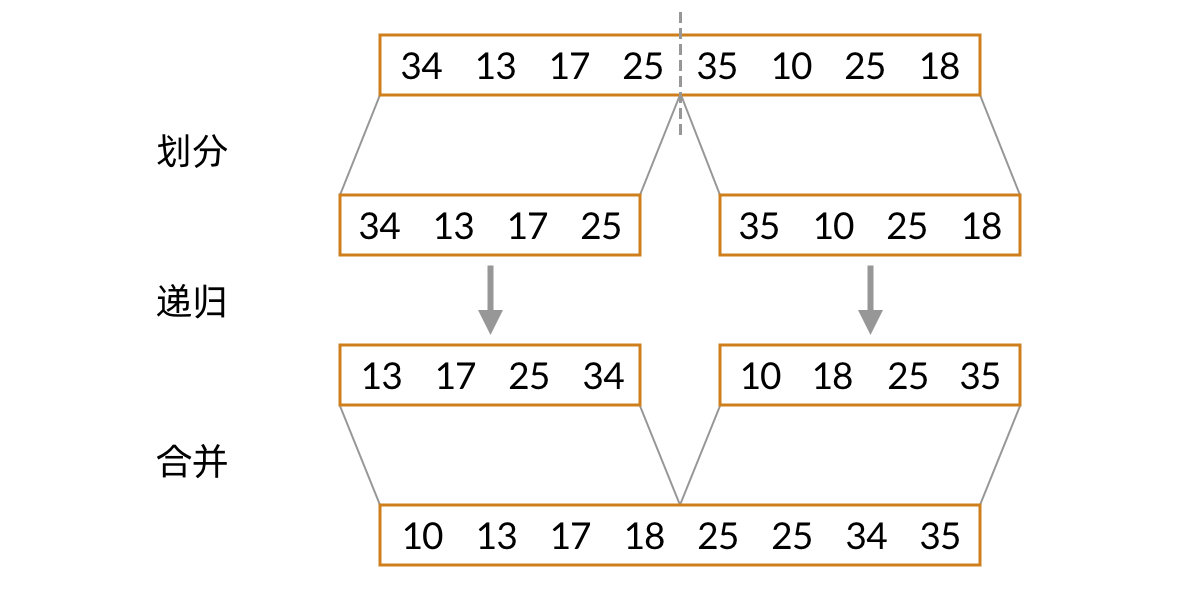
分治的归并排序算法

根据 master theorem，这样的分治算法的时间复杂度是 $O(n \log n)$ 。

那么应用到链表上，这个算法是什么样子的呢？

划分：因为不能随机访问链表中点，需要做一次顺序遍历，需要 $O(n)$ 的时间；
递归：和数组排序一样；
合并：只需要用顺序遍历就可以做到，和数组排序一样， $O(n)$ 的时间。

可以看到，虽然划分阶段的用时从 $O(1)$ 变成了 $O(n)$ ，但是这没有超过合并阶段的时间。由于 master theorem 是看划分和合并阶段的总时间的，链表排序的时间复杂度和数组排序一样，都是 $O(n \log n)$ 。在时间复杂度这里我们达到了要求，接下来就是看看每一个步骤具体如何操作。

链表切分

链表的切分需要将链表平分为左右两半。这个操作实际上可以拆分为两个基本操作：

寻找链表的中点
删除链表中点左侧的指针，将链表断开

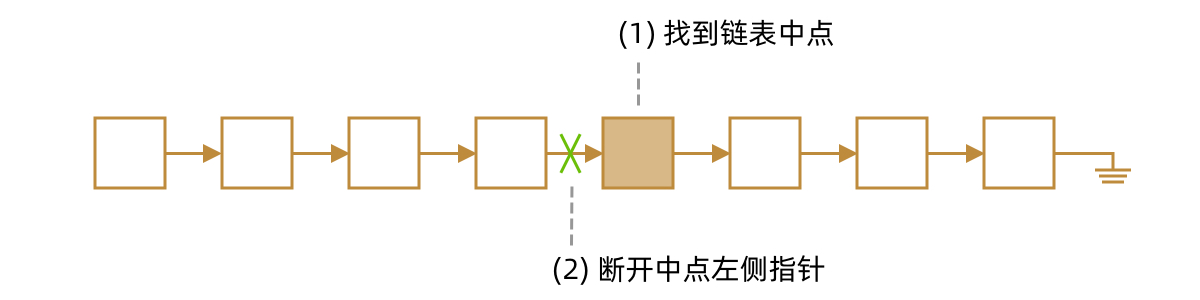
链表切分的两个步骤

寻找链表中点的操作，我们在链表快慢指针的文章中讲过，使用一快一慢两个指针遍历链表即可。

删除链表指针，实际上和删除链表结点类似。我们在链表遍历框架的文章中讲过，使用相邻的两个指针一同遍历链表即可。

那么如何将这两个方法融合起来呢？我们使用三个指针即可，分别是快指针、慢指针、慢指针的前一个指针。这样当快指针到达链表尾部时，慢指针的前一个结点正好是我们要删除的指针。

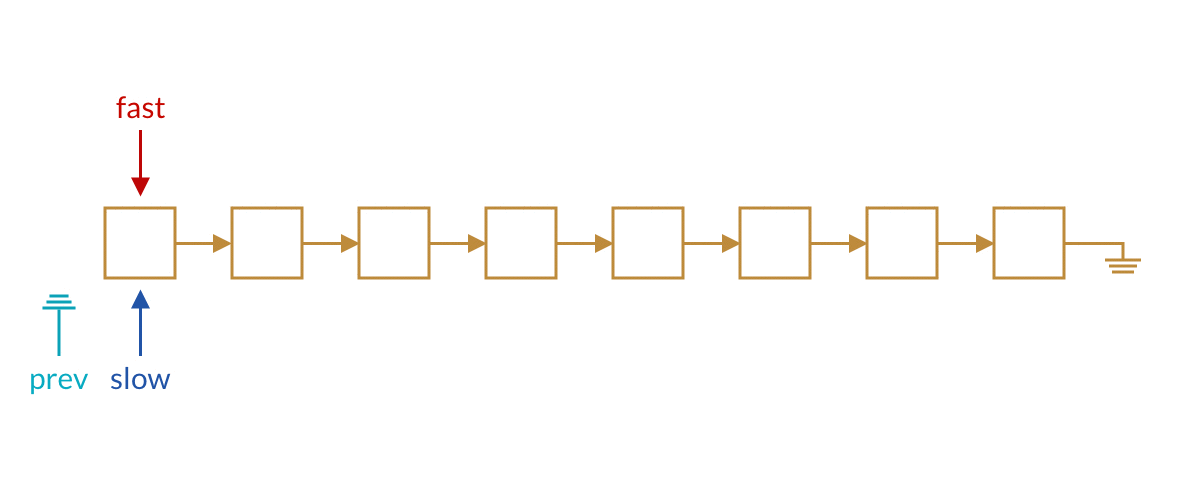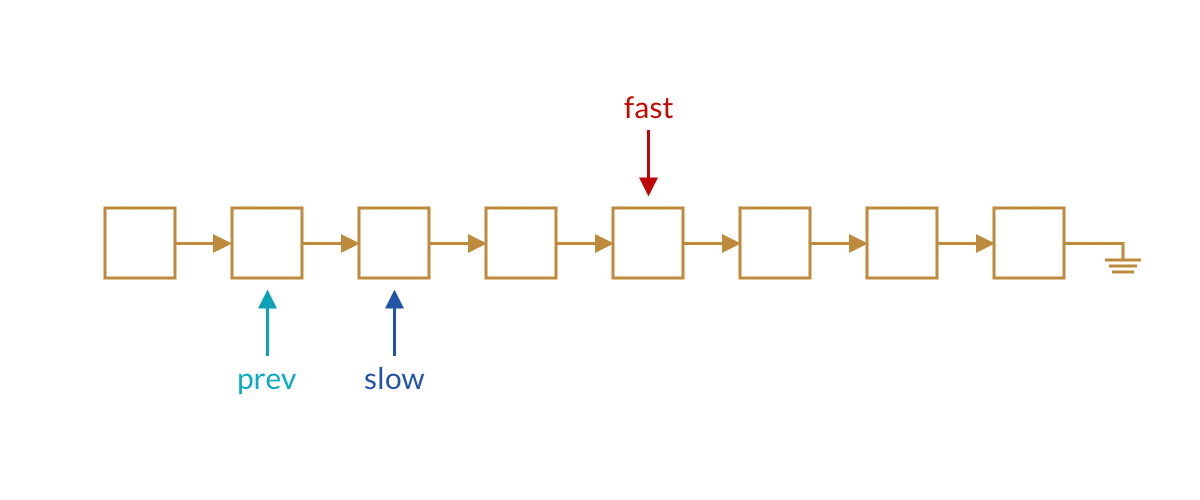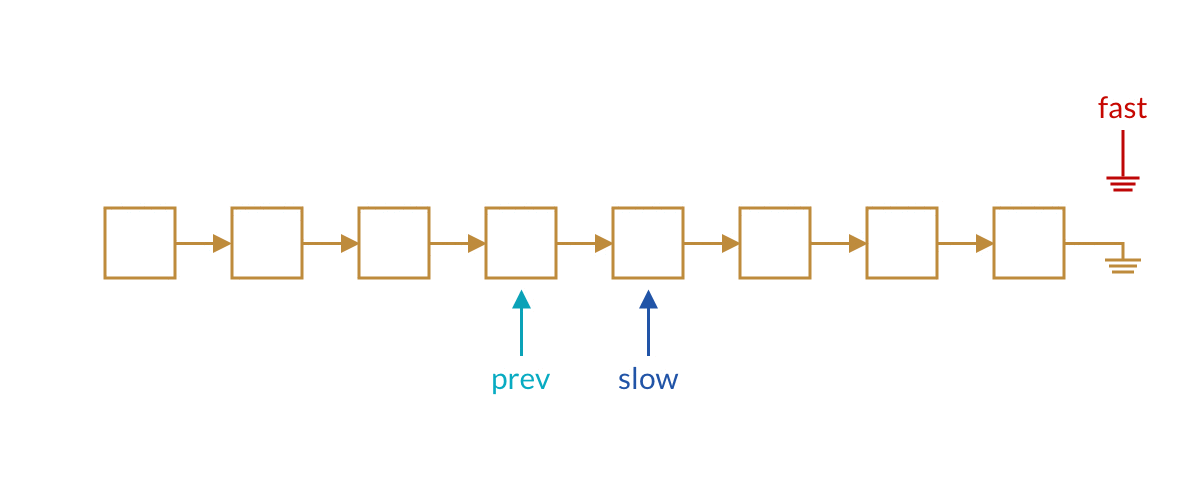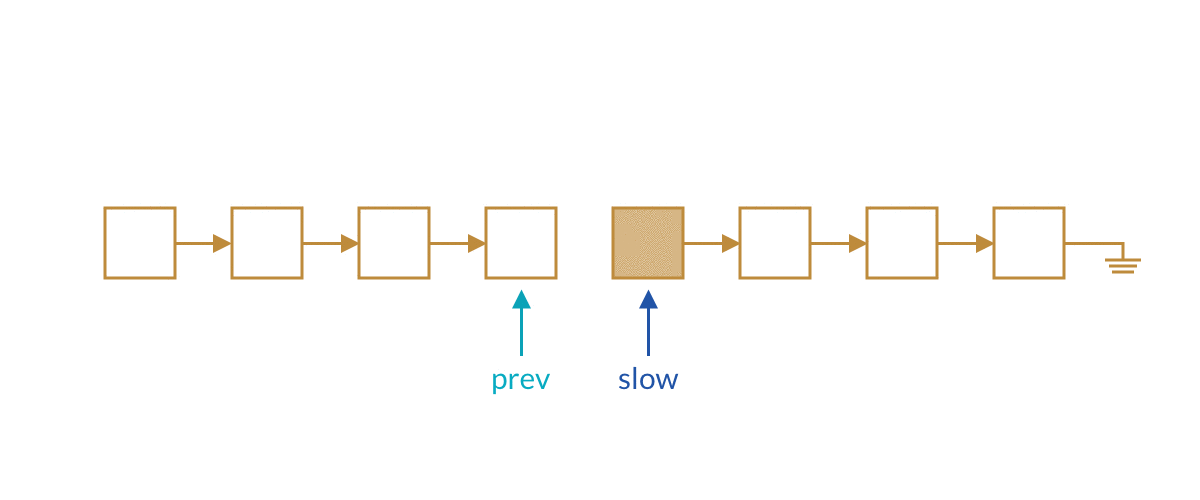
三个指针的移动过程

ListNode split(ListNode head) {
    ListNode fast = head;
    ListNode slow = head;
    ListNode prev = null;
    while (fast != null && fast.next != null) {
        fast = fast.next.next;
        prev = slow;
        slow = slow.next;
    }
    prev.next = null; // 将链表断开
    return slow;
}

虽然代码中的指针操作很复杂，但只要理解了链表的两种双指针基本操作，写起来还是无压力的。

链表合并

如何将两个有序的链表合并成一整个有序链表呢？其实，链表的合并也是一种基本操作，例如这一题，考的就是链表合并：

LeetCode 21 - Merge Two Sorted Lists（Easy）

如果你没做过这道题，那么也没关系，我们来看看数组版归并排序的代码是怎么写的。以下代码摘自 Sedgewick 的《算法4》：

void merge(Comparable[] a, Comparable[] aux, int lo, int mid, int hi) {
    // copy to aux[]
    for (int k = lo; k <= hi; k++) {
        aux[k] = a[k]; 
    }

    // merge back to a[]
    int i = lo, j = mid+1;
    for (int k = lo; k <= hi; k++) {
        if      (i > mid)              a[k] = aux[j++];
        else if (j > hi)               a[k] = aux[i++];
        else if (less(aux[j], aux[i])) a[k] = aux[j++];
        else                           a[k] = aux[i++];
    }
}

可以看到数组合并的思路很简单。两个指针 i、j 分别指向两个数组中待合并的下一个元素，每次选择一个较小元素加入新数组尾部。四个条件分支分别是：

判断两个数组其中一个元素用完的情况（两个分支）
如果两个数组都有元素，比较大小（两个分支）

如果我们把上面思路中的“数组”全部换成“链表”，实际上就得到了链表合并的方法。不过链表需要不停地把结点插入到链表尾部，代码会比较啰嗦一点。

// 全局变量，用于将结点插入链表尾部
ListNode head;
ListNode tail;

ListNode merge(ListNode left, ListNode right) {
    head = null;
    tail = null;
    ListNode q1 = left;
    ListNode q2 = right;
    while (q1 != null || q2 != null) {
        if (q1 == null) {
            append(q2);
            q2 = q2.next;
        } else if (q2 == null) {
            append(q1);
            q1 = q1.next;
        } else if (q1.val < q2.val) {
            append(q1);
            q1 = q1.next;
        } else {
            append(q2);
            q2 = q2.next;
        }
    }
    return head;
}

void append(ListNode node) {
    if (head == null) {
        head = node;
        tail = node;
    } else {
        tail.next = node;
        tail = node;
    }
}

全部代码

到了这里，链表排序的全部代码已经完成了。下面是完成的题解代码：

public ListNode sortList(ListNode head) {
    if (head == null || head.next == null) {
        return head;
    }
    ListNode mid = split(head);
    ListNode left = sortList(head);
    ListNode right = sortList(mid);
    return merge(left, right);
}

ListNode split(ListNode head) {
    ListNode fast = head;
    ListNode slow = head;
    ListNode prev = null;
    while (fast != null && fast.next != null) {
        fast = fast.next.next;
        prev = slow;
        slow = slow.next;
    }
    prev.next = null;
    return slow;
}

ListNode head;
ListNode tail;

ListNode merge(ListNode left, ListNode right) {
    head = null;
    tail = null;
    ListNode q1 = left;
    ListNode q2 = right;
    while (q1 != null || q2 != null) {
        if (q1 == null) {
            append(q2);
            q2 = q2.next;
        } else if (q2 == null) {
            append(q1);
            q1 = q1.next;
        } else if (q1.val < q2.val) {
            append(q1);
            q1 = q1.next;
        } else {
            append(q2);
            q2 = q2.next;
        }
    }
    return head;
}

void append(ListNode node) {
    if (head == null) {
        head = node;
        tail = node;
    } else {
        tail.next = node;
        tail = node;
    }
}

总结

链表排序问题并不难，但是作为综合题，考察的是方方面面的知识。我们需要理解链表遍历框架、链表快慢指针这些基本操作，还需要清除链表的性质，选择合适的排序算法，并从已有的数组排序方法中迁移知识。如果你要准备面试的话，不妨把这道题做熟练了，对于链表类问题是一个很好的总结。

排序思路
- 选择排序方法
- 将归并排序迁移到链表
链表切分
链表合并
- 全部代码
总结