基本操作的威力：以 reverse 为例

2434 字

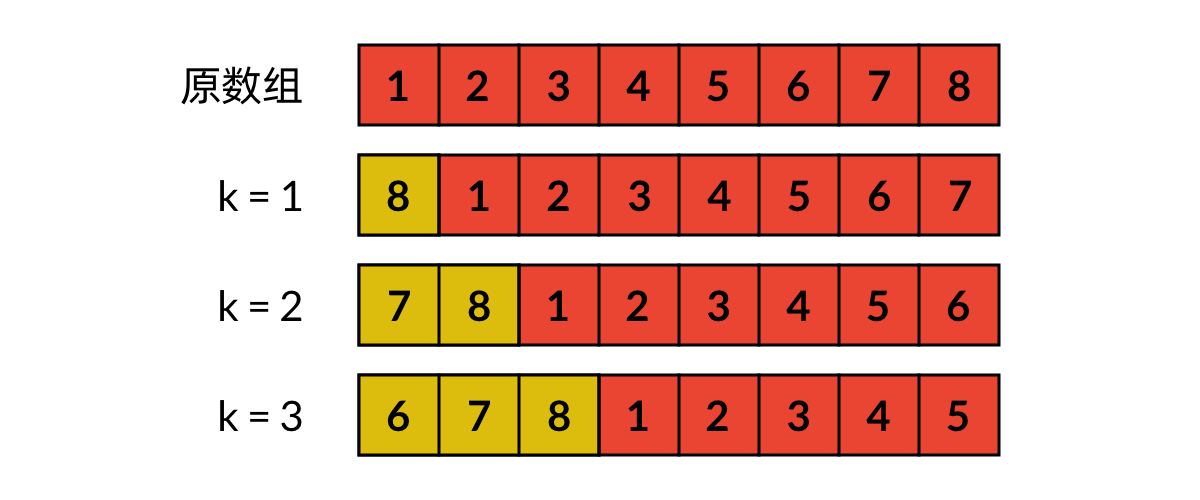
本期例题：LeetCode 189 - Rotate Array（Easy）

给定一个数组，将数组中的元素向右移动 k 个位置，其中 k 是非负数。

旋转数组是一道非常经典的题目，也是一个典型的“看过答案才恍然大悟”的题目。在准备面试的时候，这道题目是不可不知的。

你也许已经知道这道题的解法，也许一无所知。不过，本篇文章的重点不是讲解这道题。题目本身的答案不重要，重要的是能够分析其背后的原理，举一反三。本文将分析这个题目如何由基本操作得来，以及基本操作的威力。

这篇文章将会包含：

本期例题的多种解法
reverse 操作的多种应用
何为基本操作
相关题目与参考资料

旋转数组问题的解法

下面将展示旋转数组的三种不同的解法。

解法1：使用额外空间

这是最普通的一种解法。我们可以使用一个辅助数组存储原数组末尾的 k 个数字，然后再移动剩下的数字。数字移动的过程如下所示。

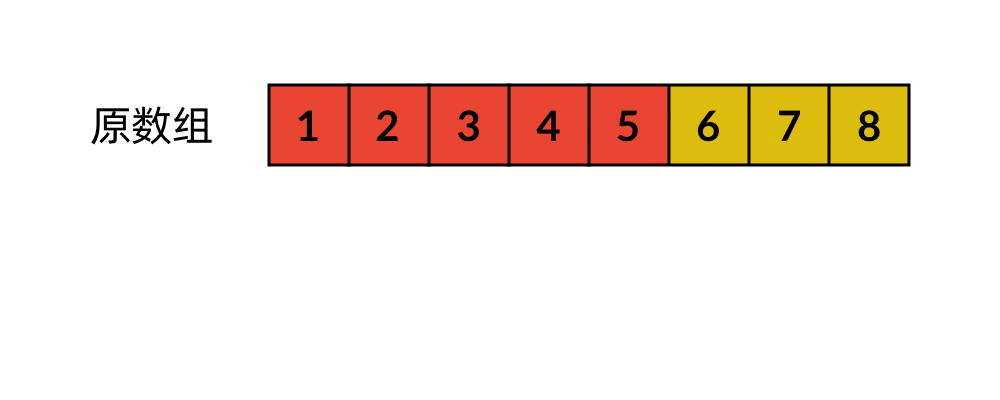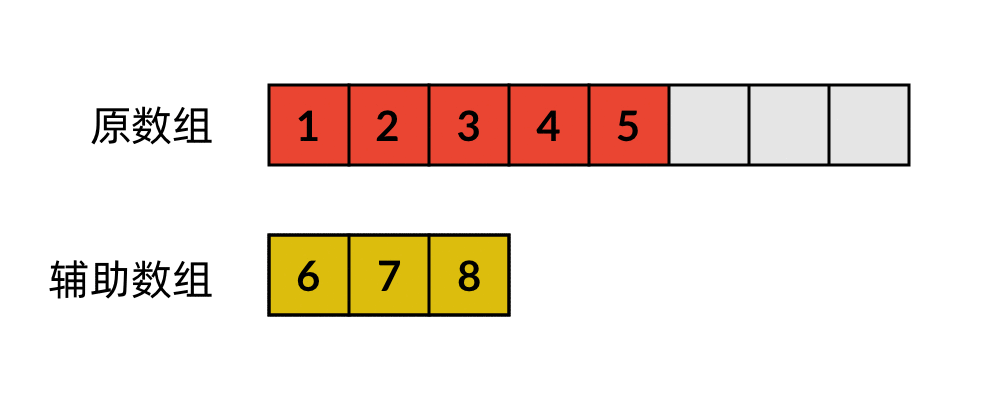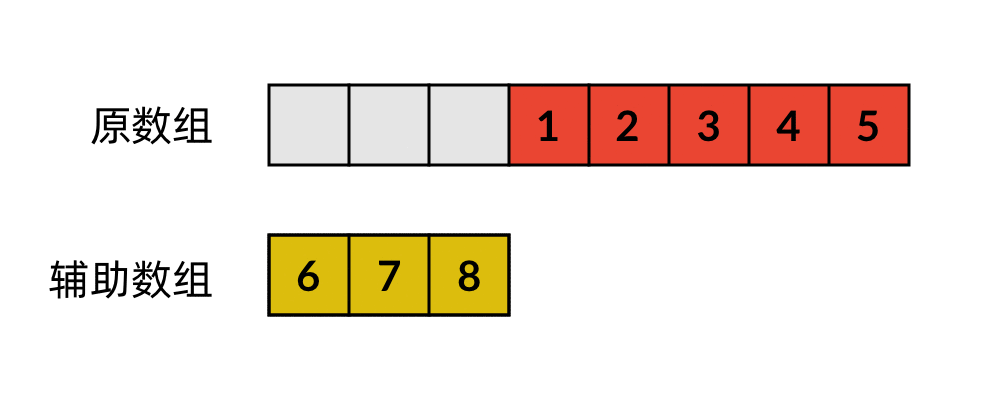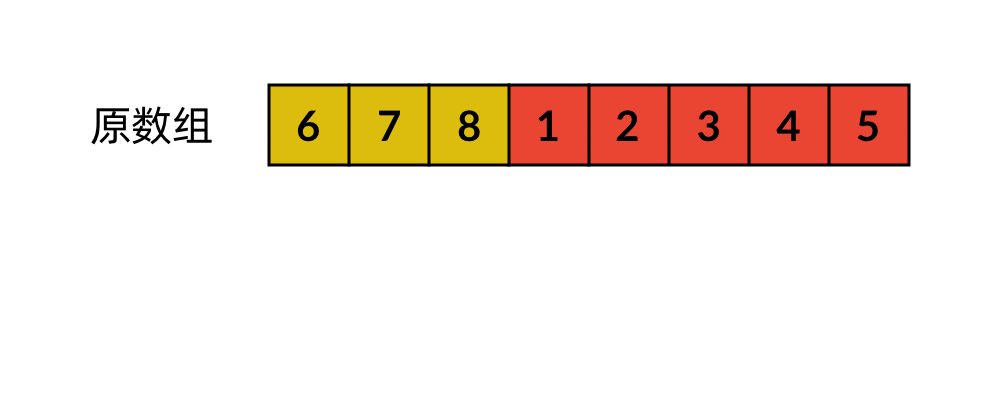
使用辅助数组进行移动

这种解法的时间复杂度是 $O(n)$ ，空间复杂度是 $O(k)$ 。很显然，它使用了额外的空间，还可以进一步优化。

解法2：环状替换

有些人首先想到的是这个思路。我们可以轻松推出每个数字最后应该在的位置，那么就可以一个一个地把它们放到正确的位置上。以 $n=7$ 、 $k=2$ 为例，移动的顺序是：1 ➝ 3 ➝ 5 ➝ 7 ➝ 2 ➝ 4 ➝ 6 ➝ 1。如下图所示，所有的箭头构成了一个环。

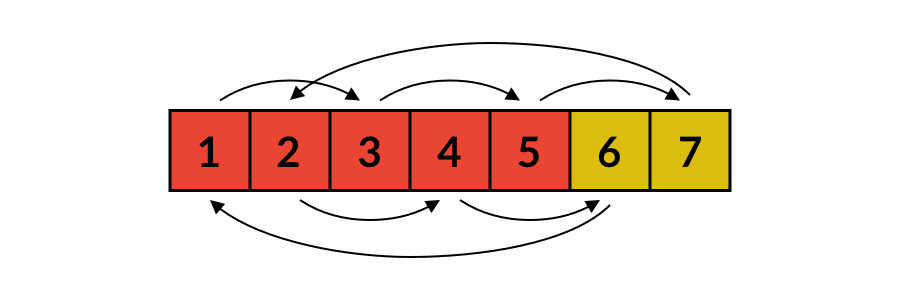
n=7, k=2 时的环状替换过程

那么我们的替换方法是：先用临时变量保存 1，将 6 放到 1 处，再将 4 放到 6 处…… 以此类推，最后将 1 放到 3 处。

不过，这种解法的正确性不容易证明。实际上，当 $n$ 是 $k$ 的倍数时，上面的这种替换方法并不成立。如下图所示，当 $n=8$ 、 $k=2$ 时，实际上存在两个环：

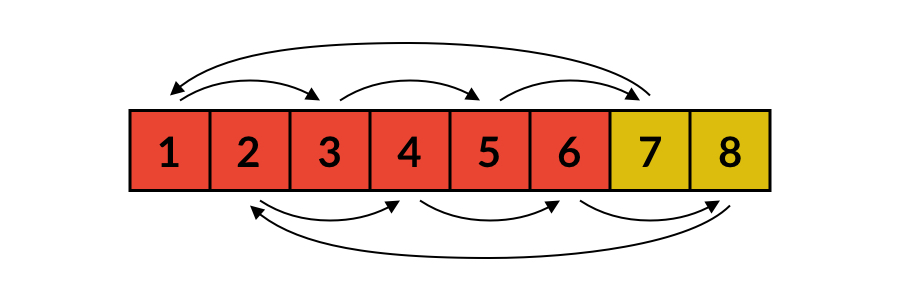
n=8, k=2 时的环状替换过程

1 ➝ 3 ➝ 5 ➝ 7 ➝ 1
2 ➝ 4 ➝ 6 ➝ 8 ➝ 2

如果从 1 出发，将只能替换 1、3、5、7 四个数，还需要再从 2 出发一遍。可见这种思路在实现上也比较麻烦。虽然这种方法达到了 $O(n)$ 的时间复杂度和 $O(1)$ 的空间复杂度，但是由于证明和实现上的复杂，并不推荐。

解法3：reverse 操作

可能你已经知道了 reverse 操作的解法，如果你还不知道的话，那么这个解法会让你恍然大悟，就像 Two Sum 问题的那个双指针解法一样。先将整个数组反转，再将数组的前后两半（前 k 个数和后 k 个数）分别反转，就可以实现数组的旋转了。

三次反转（reverse）操作的过程如下图所示：

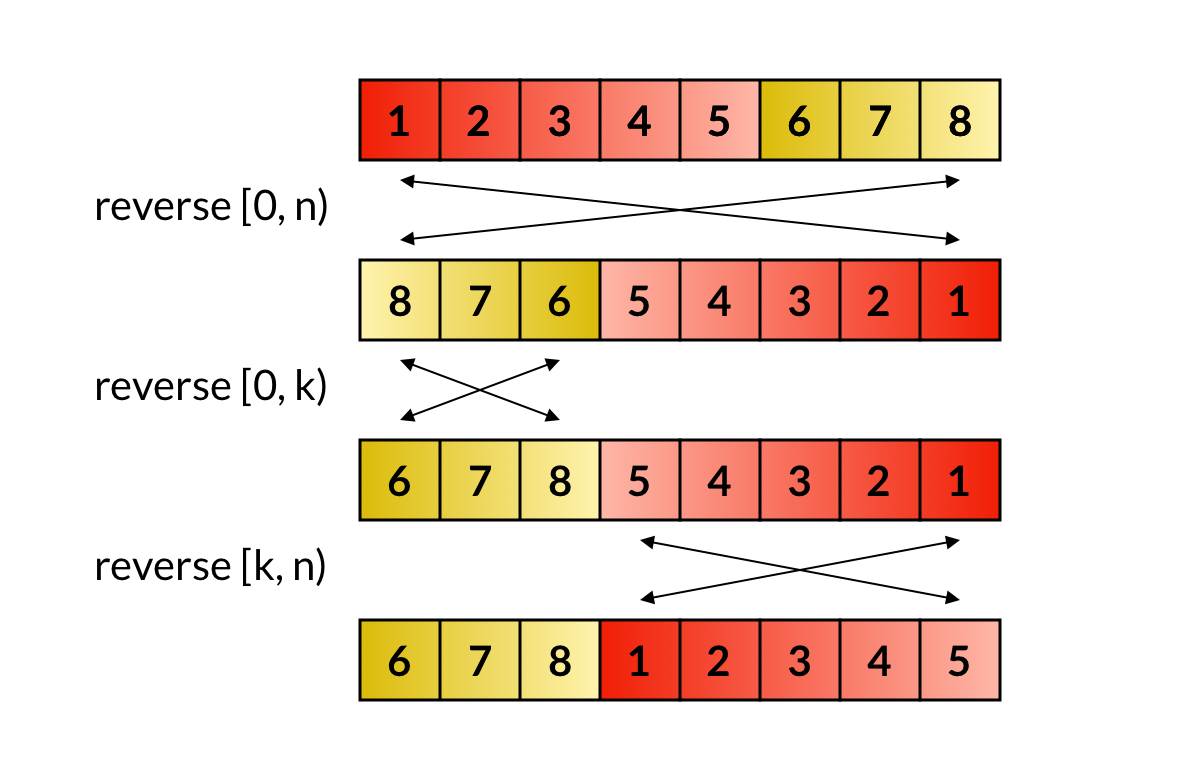
三次反转操作的过程

相应的代码如下，非常简单明了。这个解法容易理解、容易证明、容易记忆，又能达到最好的 $O(n)$ 时间、 $O(1)$ 空间，可以说是最完美的解法。

public void rotate(int[] nums, int k) {
    int N = nums.length;
    k %= N;
    reverse(nums, 0, N);
    reverse(nums, 0, k);
    reverse(nums, k, N);
}

void reverse(int[] nums, int begin, int end) {
    for (int i = begin, j = end - 1; i < j; i++, j--) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

基本操作的威力

这个三次 reverse 的解法，确实巧妙而有效，但是，如何能自己想出这个解法呢？似乎除了“见多识广”之外，并没有更好的方法。当然，还有一种方法是对 reverse 这样的基本操作十分熟悉。这道题我们的目标是达到 $O(n)$ 的时间复杂度， $O(1)$ 的空间复杂度。而如果我们对 reverse 操作熟悉，知道它同样是 $O(n)$ 时间、 $O(1)$ 空间的操作，就可以思考能否用 reverse 做到。

如果直接让你写一段反转数组的代码，那么每个人都可以轻松写出，然后分析它的时间空间复杂度。但是如果我们没有把反转数组视为一个基本操作，就无法举一反三，应用到其他题目中。

心理学家曾研究过，人的短期记忆长度大约为 7 个单位。通俗地说，我们思考问题时的“工作台”（或者比喻为“缓存大小”）是有限的。如果将 reverse 视为一个基本操作，则旋转数组这个问题只需要考虑三个操作之间的组合关系。而如果 reverse 要看成若干个操作的组合，大脑中的工作台就放不下这么多操作，也就很可能想不出问题的答案。

上面的题解代码中也是遵循“基本操作”的原理，将 reverse 写为单独的函数，这样核心的代码就只有三行了。实际上，如果是熟悉 C++ 的人，会知道 C++ 中就有现成的反转数组操作 std::reverse，用这个写出来的题解代码非常简洁：

void rotate(vector<int>& nums, int k) {
    k %= nums.size();
    reverse(nums.begin(), nums.end());
    reverse(nums.begin(), nums.begin() + k);
    reverse(nums.begin() + k, nums.end());
}

没错，如果说在其他语言中，reverse 还只是一种思路上的基本操作的话，在 C++ 中，reverse 已经是一种语言上的基本操作。这更能体现基本操作是如何减轻思维上的负担的。当然，我不是在宣扬 C++ 有多好，不过多接触不同的语言确实是有好处的，有时候能跳出当前语言的一些局限性，避免让语言的局限成为思维上的束缚。

像 reverse 这样的基本操作还可以有很多：

在有序数组中搜索一个数，需要 $O(\log n)$ 的时间（二分搜索）
在数组中以一个枢纽元素为基准划分为大小两半，需要 $O(n)$ 的时间（快速排序的 partition 步骤）

除此之外，我们学习过的堆、平衡二叉搜索树、散列表的各项时间、空间复杂度，都是基本操作的例子，它们不仅对分析算法的复杂度有帮助，更在我们设计算法的时候起到重要的作用。

reverse 操作的更多应用

旋转数组有一道推广题目，反转单词：LeetCode 151 - Reverse Words in a String（Medium）

将字符串中的单词顺序进行反转。例如：

输入："the sky is blue"

输出："blue is sky the"

如果你刚刚做过反转数组，那么应该能够轻松想出这道题的思路。这道题的解法思路其实和旋转数组是相同的：先做整体的反转，再做每个单词的反转。过程如下图所示。

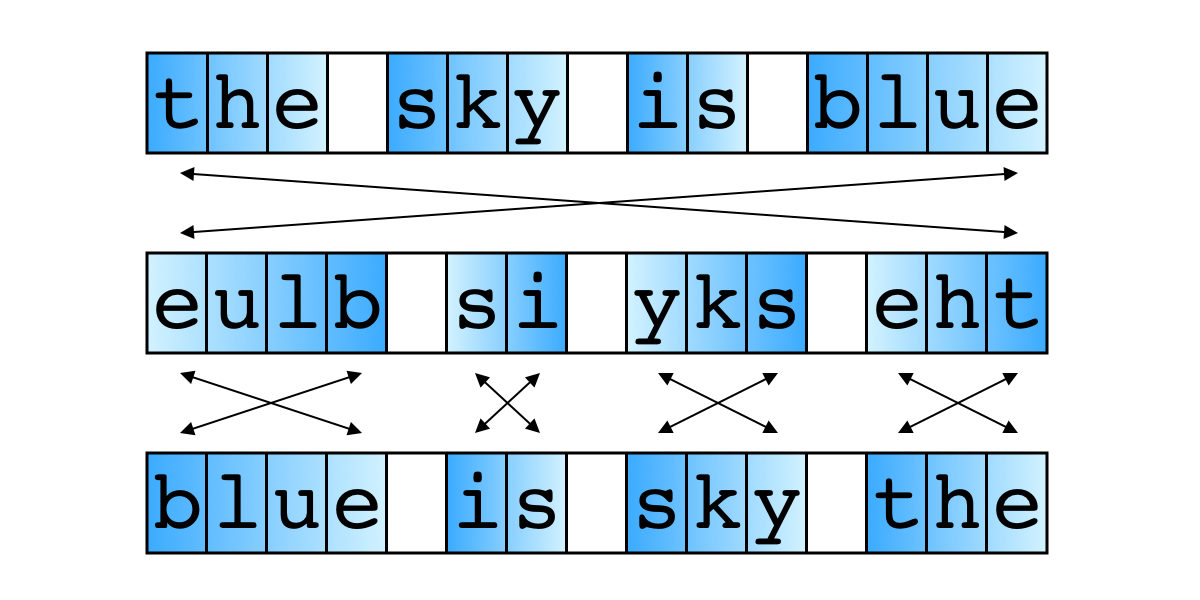
反转操作的过程

另外，reverse 操作还可以用在一些字符串和数字转化的题目中。例如：

LeetCode 415 - Add Strings（Easy）

计算两个字符串形式的非负整数的和。

LeetCode 504 - Base 7（Easy）

给定一个整数，将其转化为7进制，并以字符串形式输出。

无论是做加法还是进制转换，都是先计算结果的低位数字，再到高位数字。而输出的是字符串形式，这意味着要不断在字符串的开头插入字符，时间开销很大。

一种解决方法是使用数组或栈来临时保存结果的每一位数字，最后再输出成字符串。当然还有另一个更简单的方法：直接输出一个“反着的”结果字符串，最后再将字符串反转即可。

总结

《编程珠玑》第 2.3 章中讲到了同样的旋转数组问题。本篇的标题“基本操作的威力”正是使用了书中的标题。书中提到了一个实际的例子：文本编辑器中“行的移动”的操作，实际上就是数组的旋转。使用 reverse 操作实现的代码，一次就可以正确运行，而基于链表的代码则有几个 bug。这是本文中没有提到的、基本操作的另外一个例子：更容易实现。

“容易想出解题思路”和“容易写出实现代码”其实是相辅相成的。因为代码实际上就是思路在纸上的落实。我们在面试中，需要锻炼这种能在有限时间内写出正确的、bug-free 代码的能力。所以我们在做题的时候，需要重点掌握的不是那些最快速、最花哨的解法，而是思路最清晰、代码最简洁的解法。

本篇文章以 reverse 为例讲述了基本操作的重要作用，希望你能在做题的过程中总结出更多的基本操作。下篇文章是姊妹篇，将介绍“基本数据结构”的作用，敬请期待。

旋转数组问题的解法
基本操作的威力
reverse 操作的更多应用
总结