变位词问题：基本数据结构的威力

2256 字

本期例题：LeetCode 242 - Valid Anagram（Easy）

给定两个字符串 s 和 t ，判断 t 是否是 s 的变位词，即是否可以将 s 中的字母重新排列来得到 t。

在上一篇文章中，我们讲述了“基本操作”对于解题思路的重要作用。本篇文章讨论的主题相似，将讲述“基本数据结构”的作用。

不少同学在刷 LeetCode 题目的时候，会只关注算法的技巧，而忽视数据结构的作用。其实不然，数据结构是算法的基础。不论是那些你觉得过于简单的栈、队列，还是你可能不怎么掌握的并查集，都在对于很多算法题的思路非常重要。

本篇文章不讲高深的数据结构，本期例题也很简单。只是借这道题，举一个每个人都会用到、但常常会忽视的数据结构 counter，以此一窥基本数据结构的威力。

这篇文章将会包含：

变位词问题的不同解法
counter 数据结构的应用
何为基本数据结构
相关题目

变位词问题的解法

解法1：排序

变位词使用相同的字母，只是顺序不同。所以，如果对字符串进行排序的话，互为变位词的两个字符串应当得到同样的排序结果。

变位词排序后得到相同字符串

排序方法的最大好处是，它甚至可以找出一个字典（单词集合）中所有的变位词。我们首先对每个单词排序计算它的“签名”，再对签名进行排序，签名相同的单词即互为变位词。过程如下图所示。

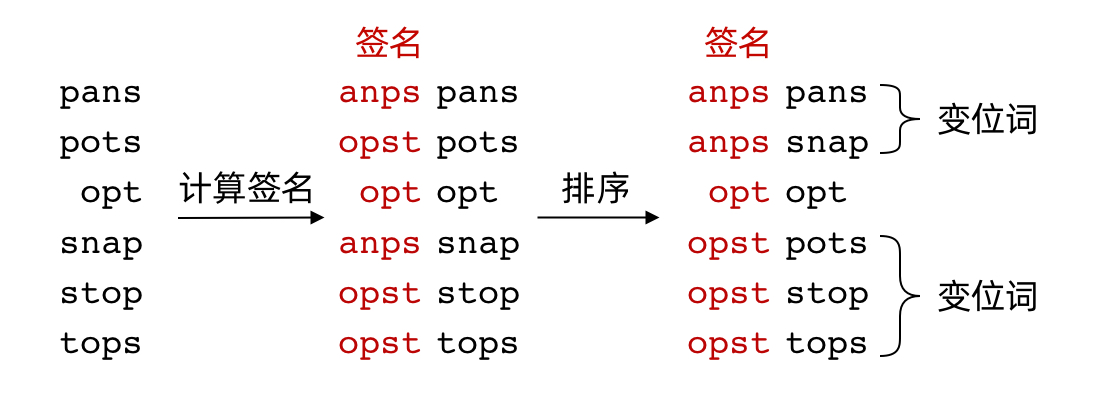
找出字典中所有的变位词

不过排序需要 $O(n \log n)$ 的时间复杂度。如果只是比较两个字符串是否是变位词的话，用计数的方法其实更有效。

解法2：计数

如果对字符串中字符的出现此处进行统计，显然互为变位词的两个字符串应当得到同样的统计结果。

变位词计数后得到相同数据

那么，我们使用对字符串中的字符进行计数，并比较各个字符的计数是否相等即可。

**语言小贴士：**在不同的语言中该用什么数据结构来计数？

在 C++ 中，使用 unordered_map。C++ 的 map 在使用 [] 时，如果 key 不存在，会自动创建默认值 value，这个特性让计数操作很简单。
unordered_map<char, int> counter;
for (char c : word) {
    counter[c]++;
}
在 Java 中，使用 HashMap。HashMap 的 getOrDefault 方法可以在 key 不存在的时候使用默认值。
Map<Character, Integer> counter = new HashMap<>();
for (int i = 0; i < word.length(); i++) {
    char c = word.charAt(i);
    counter.put(c, counter.getOrDefault(c, 0) + 1);
}
在 Python 中，使用字典。
counter = {}
for c in word:
    if c not in counter:
        counter[c] = 0
    counter[c] += 1

我们使用 Python 写出的题解代码为：

def isAnagram(self, s: str, t: str) -> bool:
    counter = {}
    # 对 s 中出现的字符，增加计数
    for c in s:
        if c not in counter:
            counter[c] = 0
        counter[c] += 1
    # 对 t 中出现的字符，减少计数
    for c in t:
        if c not in counter:
            counter[c] = 0
        counter[c] -= 1
    for v in counter.values():
        if v != 0:
            return False
    return True

使用 counter 数据结构

你也许不知道，在 Python 的标准库中，有一个 Counter 类，专门用来做这种计数的工作。上面 Python 的计数方法其实完全可以用 Counter 写成这样：

counter = Counter()
for c in word:
    counter[c] += 1

或者更简洁一些，这样：

counter = Counter(word)

这让我们需要写的代码大大简化了。使用 Counter 类的话，我们的题解代码甚至可以只用一行解决：

def isAnagram(self, s: str, t: str) -> bool:
    from collections import Counter
    return Counter(s) == Counter(t)

Amazing！原本语法的限制让我们必须要写很多行的代码，而 Counter 数据结构帮助我们用一行代码就表达清楚了思路。

不过在面试中，我们还是尽量使用最常见的数据结构。我们只需要了解有 Counter 这样的数据结构存在即可，它的存在更多是为了帮助我们理清思路，而非简化代码。上面的代码中虽然是使用 map 来计数，但变量名是 counter，就是理清思路的一种体现。

counter 与 multiset

还是同样的道理，这里我并不是在宣扬 Python 的好处。只是如果你接触不同的语言，就能发现像 Python 的 Counter 这样能简化思路的数据结构。

不过，counter 这样一个结构并不是 Python 特有。很多语言中其实有同样功能的设施，只不过名字不同。Counter 本质上是数学上的 multiset 概念。所谓 multiset，是一种变异的集合（set），它允许重复的元素出现。我们对单词中的字符进行计数，然后比较计数是否相同，其实就是在比较单词中的字符集合是否相同。

对单词字符做计数

将单词变为字符集合

如果从 multiset 的角度来看，是不是更加接近变位词这一问题的本质了呢？

在很多语言中都有 multiset 的数据结构：

C++ 可以用 std::multiset
Java 可以用 Guava 的 multiset

例如 C++ 可以这么写题解代码：

bool isAnagram(string s, string t) {
    multiset<char> counter1(s.begin(), s.end());
    multiset<char> counter2(t.begin(), t.end());
    return counter1 == counter2;
}

Java 即使用上了 multiset 也写不出简洁的代码，这里就不展示了。

如果我们对 multiset 有所了解，而且知道它可以用 map 来实现，在写题解代码的时候同样可以屏蔽语言本身的复杂性，保持思路的简单。

基本数据结构的威力

我们在上一篇文章中讲过，像 reverse 这样的基本操作，可以让你在有限的思维“工作台”中思考更多的内容。像 counter 这样的基本数据结构其实也有类似的作用，它是对数据及其操作的一种抽象，可以让你屏蔽掉一些繁杂的细节，直奔操作的主题。

基本数据结构的威力之一，是让我们可以从高于语法的角度，理解数据结构的语义。

例如， counter 我们实际上是用 map 来实现的，但 map 也可能是存储一些查找结构。而对于查找结构而言，它既可以用散列表、也可以用平衡二叉树来实现（Java 里的 HashMap 与 TreeMap）。

数据结构既可以从其底层实现描述（数组、链表、二叉树、散列表等），又可以从其高层性质描述（栈、队列、优先队列、搜索结构等）。这些高层的性质就是数据结构的语义。一个典型的例子就是“堆”与“优先队列”。堆是一种带元素调整的二叉树，但我们使用的时候，不会关注堆中调整的细节，只会关注优先队列将最小值调整到队列头的性质。

基本数据结构的威力之二，是让我们可以有更多的武器思考问题的解。

在算法题中，我认为单调栈和并查集是最能体现这一点的例子。当你了解了单调栈，就能知道“下一个更大的元素”可以用单调栈在 $O(n)$ 时间内求出来，并在解题时使用这个已知的结论。即使你需要一点时间回顾单调栈的正确写法，但你已经能把基本的解题思路想出来了。当你了解了并查集，就知道“维护等价关系”是一种可行的做法。在解题时，自然可以从这个角度思考。

总结

本篇文章以 counter 为例讲述的基本数据结构的重要作用。使用 counter 数据结构的题目有不少，这里列举几例：

基本数据结构也许不如基本操作更常见、更直观，但同样在总结解题思路时很有用。本文讨论的 counter 数据结构虽然很简单，但可以起到抛砖引玉的作用。后续会有专门的文章讲解更有难度、作用更大的数据结构，如单调栈、并查集、线段树等算法题中常见的数据结构，敬请期待。

变位词问题的解法
基本数据结构的威力
总结